Кључна разлика: Тачка је тачка која означава локацију која је означена на бесконачном простору или равној површини. Сматра се да је линија једнодимензионална и уведена је да представља равне објекте без ширине и дубине. Равнина је дводимензионална равна површина која је неограничено велика са нултом дебљином.
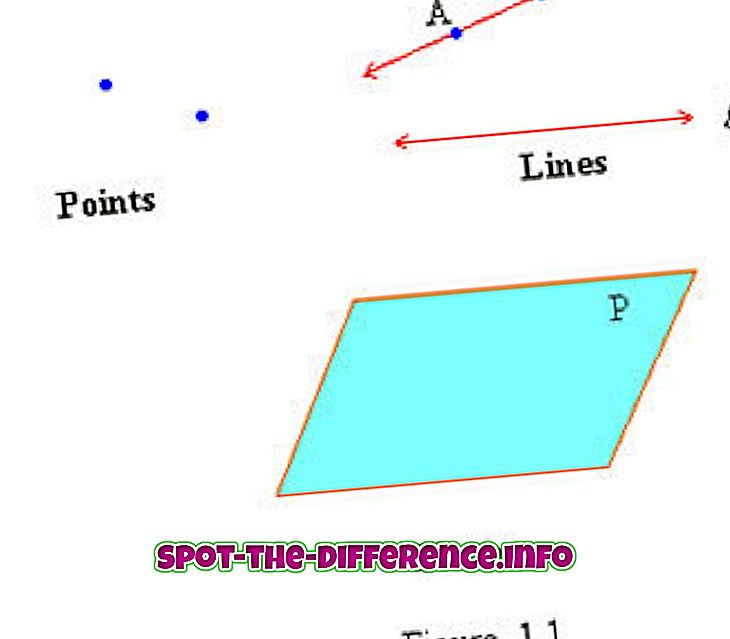
Тачке, линије и равни сматрају се недефинисаним терминима геометрије јер нису формално дефинисане. Када дефинишемо појам, обично се користи једноставнија ријеч за описивање термина. Међутим, тачка, линија и равнина се сматрају већ поједностављеним терминима. Сви остали геометријски концепти су изграђени на тачки, линији и равни. Међутим, покушајмо да разумемо ова три недефинисана термина.
Тачка је тачка која не означава ствар, већ позицију. Тачка представља локацију која је обележена у бесконачном простору или на равној површини. Тачка може бити тачка било које величине, али нема никакву дужину, ширину или дебљину. То је зато што представља место, а не ствар.
Тачке се називају коришћењем једног слова великог слова, као што су А, Б, Ц, итд. У дводимензионалном еуклидском простору, боље познатој као решетка или граф са к-осом и и-осом, тачка је представљена наручени пар (к, и). Кс представља хоризонтални положај тачке, док и представља вертикални положај. Постоје два сета тачака: колинеарни и копланарни. Колинеарни скуп тачака лежи у правој линији, док копланарни скуп линија лежи на истој равни.
Сматра се да је линија једнодимензионална и уведена је да представља равне објекте без ширине и дубине. Дефиниција линије се мења у зависности од типа геометрије. У геометрији Еуклида, линија нема дефинисану поставку. У аналитичкој геометрији, линија у равни је дефинисана као скуп тачака чије координате задовољавају задату линеарну једначину. У геометрији инцидената, линија може бити независан објекат из скупа тачака које леже на њему.
Линија се прихвата као једнодимензионални бесконачни скуп тачака које су повезане. Правац је најкраћа раздаљина између било које две тачке на равни. Линије су означене са две стрелице на крају сваке, да би означиле да се никада не завршава. Линије су именоване на два начина: по две тачке на линији или једним малим курзивним словом. Било које две тачке означене на линији могу се користити за упућивање на линију. На пример: Линија са тачкама Х, И на њој ће бити означена линијом ХИ и она ће бити постављена на врху да означи да је линија.
Равнина је дводимензионална равна површина која је неограничено велика са нултом дебљином. Авион се посматра као дводимензионални аналог тачке (нула димензија), линија (једна димензија) и чврста (тродимензионална). Када се разматра дефиниција у смислу еуклидског простора, раван се односи на цијели простор. Замислите лист метала који нема дебљину, међутим, он траје заувек. То се сматра авионом.
Википедија наводи: "Многи основни задаци из математике, геометрије, тригонометрије, теорије графова и графова се изводе у дводимензионалном простору, или другим ријечима, у равнини." ивице. Ове равни су нацртане од стране два паралелна пара и изгледају као коси правоугаоник. Авион има две димензије: дужину и ширину. Али пошто је авион бескрајно велик, дужина и ширина се не могу мерити.
Авиони су дефинисани са три тачке. Постоје две врсте равни: паралелне и пресечне равни. Паралелне равни су две или више равни које се крећу бесконачно без прелажења међусобних стаза. Замислите старији метални лим, сада додајте још један метални лим који се налази изнад њега и такође траје заувек. Ова два би направила две паралелне равни које се никада не укрштају. Међутим, интересантни авиони су управо то. Ово су две равни које прелазе једна другу. Авиони су обично названи са једним великим словом написаним у курзиву (Плане П).
У геометрији се тачка, линија и раван спајају у облику постулата. Овај постулат је скуп три претпоставке (аксиоми) које се могу користити као основа за еуклидску геометрију у три или више димензија. Три претпоставке укључују: Јединствена претпоставка линије, претпоставка о бројевној линији и претпоставка димензије. Јединствена претпоставка линије указује да постоји тачно једна линија која пролази кроз две различите тачке. Претпоставка о бројевној линији наводи да је свака линија скуп тачака које се могу ставити у међусобну кореспонденцију са стварним бројевима. Свака тачка може да одговара 0 (нула) и свака друга тачка може да одговара 1 (један). Коначно, димензије претпостављају стање дате линији у равни, постоји барем једна тачка у равни која није на линији. С обзиром на раван у простору, постоји барем једна тачка у простору која није у равни.